Chapter 9: Ontological Systemicity Mapping‑ A Tool for Ethical Engagement

In this chapter we focus on ontological systemicity mapping. Systemicity is defined as unfinished, unfinalized, fragmented, and less than 'whole' system (Boje, 2008, 2014). To map a systemicity is to enter the field of multi-fractality. Rather than a single fractal to define ethical engagement, there is multi-practality, polyphnic fractality, and some would add, posthumanist fractality, where the point of view is not the human-species, rather it is all species, each with rights to survive.

Henri Savall and Veronique Zardet developed the theory, method, and practice of Tetranormalization.

Tetra means four, and normalization is seen as an alternative to standards.Norms are a tool of ethical engagement. Standards are a tool of hiearchical-disengagement.

Social norms are embodied in sociomateriality. Stanards try to shape and enforce ethics from a regulatory body, such as AACSB, ISO, World Bank, or World Trade Organization. It is important to keep this distinction between norms and standards in mind.  The distinction becomes crucial now that we have transitioned to a flexible capitalism of global marketplace from the days when the corporate bureaucracy reigned supreme.  The four kinds of tetra-norms are social norms, trade norms, economy/accounting norms and ecology /quality norms.

Figure 1 - Wings of Tetranormalization

Norms and Global Tetranormalization Susie Vrobel (2010) assumes that “each tribe lives under the influence of a single norm, common to all individuals” (p .202). In economic exchange, the assumption of a single and simple norm is assumed in e-trade (reputation-bases cooperation) by individuals loosely connected and geographically dispersed (p. 201). The common norm contributes to overall cohesiveness and identity of a tribe (p. 204). When different tribes are “'under the influence' of different norms” the overall fitness of a tribe will vary, and inter-tribe conflicts (war, etc) are assumed (p. 204).

For Vrobel (2010) “Fractal time not only nests past events into the present but also includes the notion of anticipation, which adds the idea of the future being embedded into the Now” (p. 238). They base the idea on Begsonian ‘duration’ of past nows into the present now, and on Husserl’s pretension: An anticipation of a future event. They, however favor the social over the materiality, stating that the material and semantic (social) are "anthpocentrical and thus derivatives of our subjective experience of time” (p. 238).

Vrobel is at The Institute for Fractal Reseach (Kassel, Germany) addresses the “interfacial cut assumed between the observer and the rest of the world” (p. 229). She stress our primary experiences of time (succession, simultaneity, duration & extended Now) affect our sense of “fractal space-time” (p. 229).

Vorbel's work applies to the popularity of grander narrative forms in organizaiton studies. She assumes “our inbuilt desire for complexity reduction” leads us to embed materiality in our abstracting, focusining on a few aspects, while disregarding others (p. 230). ForVrobel (2010: 230) “3rd -order cybernetics then contextualized the observer-participant ontologies of the 2nd -order domain.” In other words the subjectivity of the observer is a result of an embedding process in contextualized observer-ontologies that “takes account of both the system-context interface and the observer-involvement interface” (p. 230).

In the Newtonian reductionist approach, it is a linear “container-like time and space” that does not allow the kinds of observer frames which Einstin’s relativity or the quantum mechanics theories address. Prigogine’s complexity theory is said assign different internal times to nested systems (p. 230). The result is emergence becomes a differentiation between levels of description (LODs) by degrees and modes of involvement. Vrobel subscribes to ‘embodied cognition’ (p. 230), the observer’s internal different ion and how the observer is embedded in a context of system interfaces and involvements. She cites Lakoff and Nunez (2000).

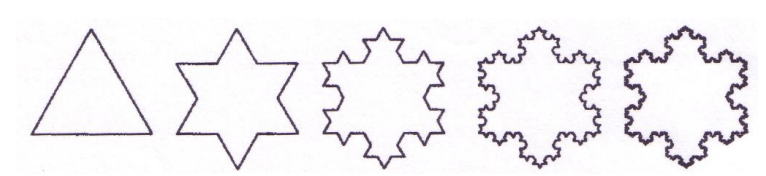
Figure 3 - Fractal Resolution INfinitesimals

In a fractal clock, there are infinitely nested number of intervals (p. 243). We can keep splitting the intervals, infinitesimally.

3 for the triangle, 12 for the 6 pointed star, then 48, 192, and 768 for the last three. In a straight line (1-dimension), the Koch curve fractal, forms a Newtonian metric (p. 243). We have a choice of five Koch curve scalability-intervals in the above figure.

Materiality in nature (coastlines, deltas, ferns, crystals, proteins etc.) only exhibited a limited scale-invariance (self-similarity) and cannot be fully realized for all scales of length (p. 243).